Orbits

Here are some examples of how to compute orbits within NEMO. First we need to select a potential. So, let's take the flat rotation curve potential with a softened core, which fits most disk galaxies, although this represents most of the spherical halo potential. Potentials are implemented via the keywords potname=, potpars= and potfile=, and all carry the same meaning accross programs. Examples of potentials in source code form are in $NEMO/src/orbit/potential/data. 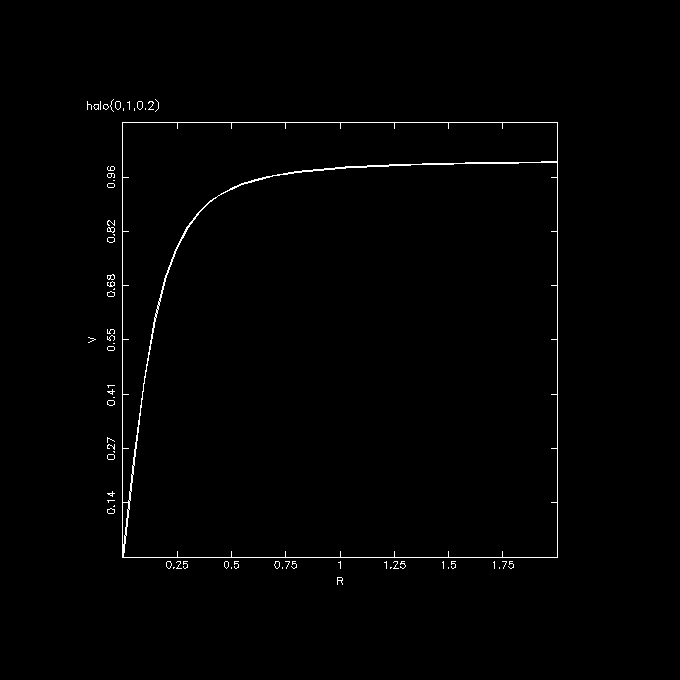For example, let us look at halo.c, which has just two parameters, the peak rotation curve and the core radius. Let us first just plot the rotation curve:

    rotcurves name1=halo pars1=0,1,1 radii=0:8:0.1

(the first parameter in pars1= is the pattern speed, which we will not use here)

Now we need to compute an orbit in this potential. You can give initial conditions (the advantage of this logarithmic potential is that there is no escape energy, so you don't need to worry about making sure the energy is negative to keep it within bounds), integrate them and vizualize the orbit as follows:

 mkorbit - 1 0 0 0 1 0 potname=halo | orbint - - 10000 0.01 | orbplot -

As you can see, this orbit is not closed, actually, it looks closed after three revolutions. For fun, you can perturb it a little bit, for example in the initial X position, and integrate it 10 times longer:

 mkorbit - 1.01 0 0 0 1 0 potname=halo | orbint - - 100000 0.01 | orbplot -

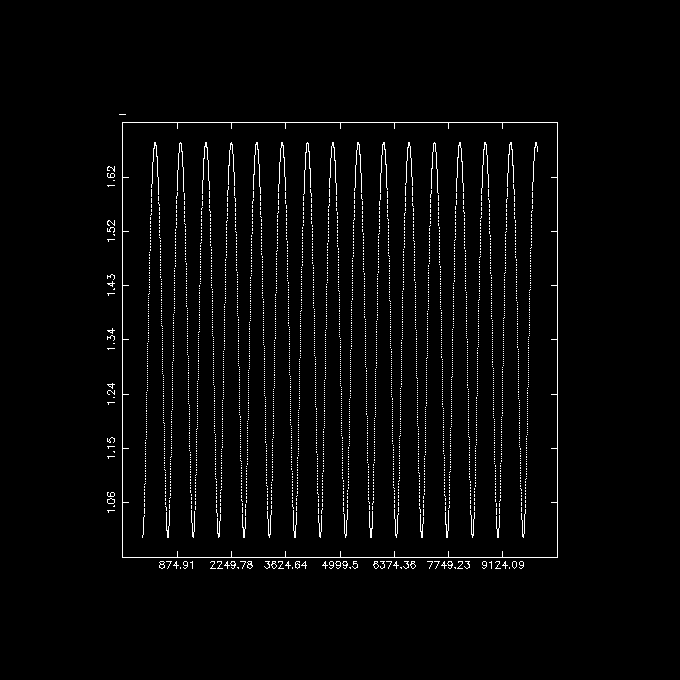
Let us plot how the radius varies with time. Since orbplot cannot handle arbitrary variables yet, we need to convert to a snapshot (where we loose time) and use the index 'i' as time. You can also choose the angular momentum (jtot), but it will be constant and 1.0 in this example.

 mkorbit - 1 0 0 0 1 0 potname=halo | orbint - - 10000 0.01 | otos - - | snapprint - i,r | tabplot -

To find a periodic orbit, you can either solve for circular orbit analytically if the potential allows this (for this potential the relationship is

 v/v0 = r/sqrt(r**2+rc**2)

or you compute them using a surface of section (orbsos) or periodic orbit finder using variational principles (perorb). For example:

 
 mkorbit - 1.01 0 0 0 1 0 potname=halo | orbint - - 100000 0.01 | orbsos - | tabplot - 3 4

or try to check if the orbit integrator can produce a circular orbit at radius 1:

 mkorbit - 1 0 0 0 '1/sqrt(2)' 0 potname=halo | orbint - - 10000 0.01 | orbplot -

Now we need to rewrite halo.c and add a small spiral perturbation.